みなさんがM3でならう「くりかえし」は、小学2年生で習う「かけ算」・小学3年生で習う「わり算」をやると理解が深まります。特に、皆さんがそんなに好きではない「文章問題」は「くりかえし」を理解するのに最高の教材です。
算数のテストの最後に出るくらいの問題を出します。「くりかえしを重ねる」にも繋がります。トライしてみてください。
問題
桃色のタイルがあります。
あなたはタイルを2枚組み合わせた形Aを床に敷き詰めるよう言われました。

形A

床
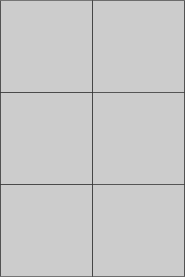
さて、タイルは何枚必要でしょうか?
解答
形Aを手前から置いていきます。
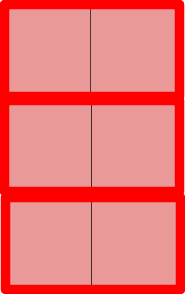
ぴったりハマりました。
Aの個数を数えてみましょう。Aは3つありますね。
では、Aに含まれるタイルの個数はいくつですか?問題文を見返すと…?「2枚」とありますね。
まとめます。
- 床を埋めるのにAは3つ必要
- Aに使われるタイルは2枚
よって
( 1つ分の数 ) ✕ (いくつ)
(Aに使うタイルの枚数)✕(Aの個数)= 必要なタイルの個数
2 ✕ 3 = 6
よって6枚です。
さて、これをプログラミングとつなげてみましょう。
プログラム化
まずは準備。
Aを作ろう
タイルを2回置いたらOKですね。この命令を追加します。
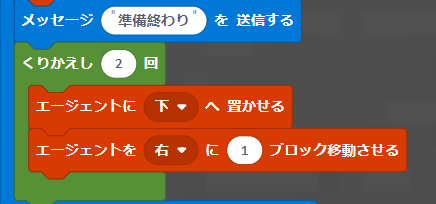
実行します。
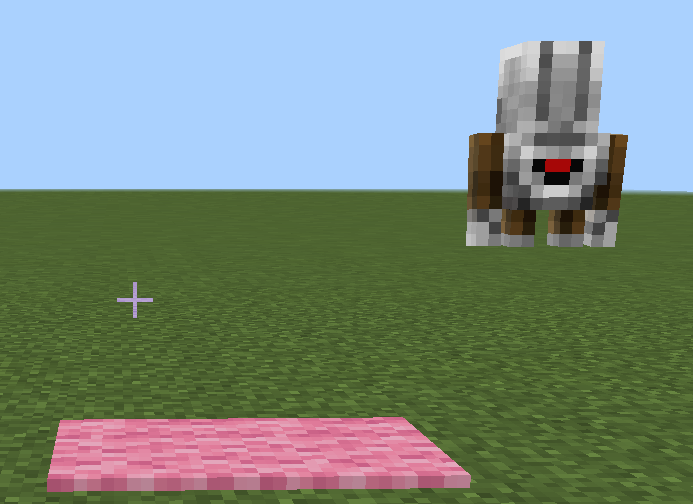
ばっちりですね。
床を埋めよう
Aのコードを繰り返します。先程、Aは3つ必要ということが分かったので、3回繰り返します。

実行してみましょう。

なんだかおかしいですね。エージェントくんには2枚置き終わったあと、左側に戻って欲しいですね。以下のように変更します。

実行すると…

床の形になりました。完成です!
プログラムを眺める
タイルの枚数の計算は下式のようになりました。
| ( 1つ分の数 ) ✕ (いくつ) (Aに使うタイルの枚数)✕(Aの個数)= 必要なタイルの個数 2 ✕ 3 = 6 |
完成したプログラムのうち、タイルを置く部分は下図のようになりました。
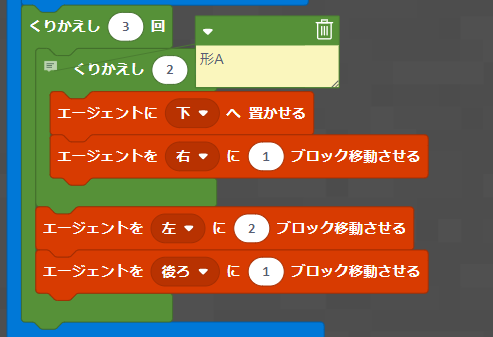
「1つ分の数」が内側の繰り返しの回数、「いくつ」が外側の繰り返しの回数と同じですね。これはたまたまではなく、算数の文章問題を、計算して解くかプログラムを使って再現するかの違いだけで、同じことをしているのです。
まとめ
今回は算数に焦点を当てましたが、他にも学校の勉強のいろいろなものをプログラムとつなげることができます。例えばM11で習う「関数」は国語の指示語(これ、あれ、それ)と、M9で習い始める「もし〇〇なら」は高校数学の論理と繋げられます。
プログラミングで知ったことを学校で、学校で知ったことをプログラミングで発揮していきましょう!
